https://www.acmicpc.net/problem/11660
1. 분류
Prefix
2. 풀이
두 점 (x1, y1), (x2, y2)으로 그릴 수 있는 직사각형의 범위 내에 있는 모든 수의 합을 구하는 문제이다.
가장 간단하게 풀 수 있는 방법은 역시나 이중 반복문으로 수를 일일이 더하는 방법일 것이다.
아쉽게도 그 방법은 사용하지 못한다.
합을 구해야 하는 갯수 M개, 행과 열의 개수 N개이므로 최악의 경우를 생각해본다면
시간복잡도는 O(M * N^2) => 100,000 * 1,024 * 1,024 = 1,048,576,000
무조건 시간초과를 유발할 것이다.
조금 다르게 생각해보자.
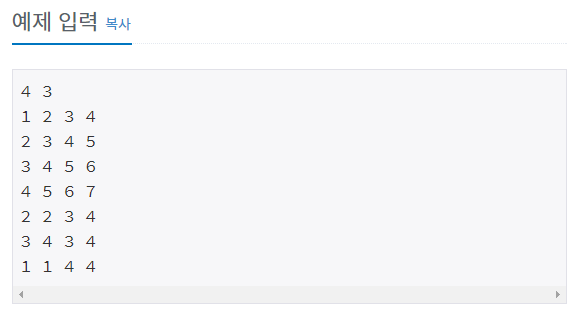
예제 입력에서 첫 번째 출력은 (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4)를 더하는 것이다.
입력을 받는 동시에 미리 더해본다면?
표의 각 두 자리 숫자는 행과 열 번호이다.
위의 표와 같이 (3, 4) = (1, 1) + (1, 2) + (1, 3) + (1, 4) + (2, 1) + (2, 2) + ... + (3, 4)로 만들면
(2, 2) ~ (3, 4) = (3, 4) - (1, 4) - (3, 1) + (1, 1)으로 다시 정리할 수 있으며
이중 반복문을 제거하기 때문에 O(M * N^2)에서 O(M * 1) => 100,000 이므로 제한시간 내에 정답을 구하게 된다.
3. 소스코드
#include <cstdio>
int t[1025][1025];
int main()
{
int n, m;
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
scanf("%d", &t[i][j]);
t[i][j] += t[i][j - 1] + t[i - 1][j] - t[i - 1][j - 1];
}
for (int i = 0; i < m; i++)
{
int x1, y1, x2, y2;
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
printf("%d\n", t[x2][y2] - t[x1 - 1][y2] - t[x2][y1 - 1] + t[x1 - 1][y1 - 1]);
}
return 0;
}
'알고리즘' 카테고리의 다른 글
| 알고리즘 Repository (0) | 2019.12.09 |
|---|---|
| BOJ [7576] 토마토 (0) | 2017.11.15 |
| 다이나믹 프로그래밍(동적 계획법) 개요 (0) | 2017.09.13 |
| 2018 1ST KAKAO BLIND RECRUITMENT 모의 테스트 문제 5 (0) | 2017.09.12 |
| BOJ [1912] 연속합 (0) | 2017.09.10 |