원문
N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.
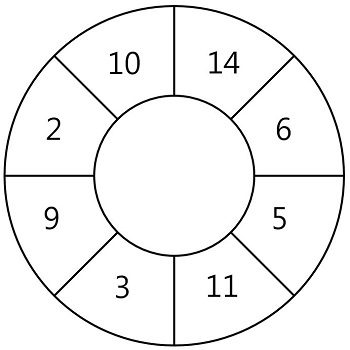
원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.
예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.
제한 사항
- sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
- sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
- 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.
입출력 예
| sticker | answer |
|---|---|
| [14, 6, 5, 11, 3, 9, 2, 10] | 36 |
| [1, 3, 2, 5, 4] | 8 |
입출력 예 설명
입출력 예 #1
6, 11, 9, 10이 적힌 스티커를 떼어 냈을 때 36으로 최대가 됩니다.
입출력 예 #2
3, 5가 적힌 스티커를 떼어 냈을 때 8로 최대가 됩니다.
1. 분류
다이나믹 프로그래밍
2. 풀이
시작점을 몰라 꽤 오랫동안 헤멘 문제였다.
첫 항부터 시작하면 마지막 항 스티커를 어떻게 해야하는지를 깊게 고민했기 때문이다.
여러 번의 시행착오 끝에 괜찮은 방법이 생각나서 잊지 않기 위해 포스트를 작성하게 되었다.
1항부터 N항까지, 각 항마다 스티커에 할 수 있는 행위는 단 두 가지이다.
1. 스티커를 떼지 않는다.
2. 스티커를 뗀다.
1번 행동을 할 때는 바로 전 항에서 무엇을 하던 상관 없으나
스티커를 한번 떼면 양 옆에 붙은 스티커를 건들 수 없다는 조건이 있기 때문에
2번 행동의 경우엔 바로 전 항에서 스티커를 떼지 않은 경우에만 가능하다.
점화식으로 표현하면 다음과 같다.
스티커를 건드리지 않을 땐 이전 항 중 최대값을 취하고
스티커를 뗄 땐 이전 항에서 스티커를 건드리지 않았을 때에 현재의 스티커 값을 더해주면 된다.
여기서 끝내기에는 문제가 있다.
첫 항과 마지막 항의 스티커를 동시에 떼어낼 수 없기 때문이다.
나는 이 문제를 두 갈래로 나누어서 해결했다.
첫 번째는 1항을 시작으로 순서대로 도는 방법,
두 번째는 마지막 항을 시작으로 거꾸로 도는 방법이다.
첫 항이 시작이면 1번 스티커부터 뗄 수 있기 때문에 마지막 스티커를 건들지 않는다(1 ~ N-1).
거꾸로 마지막 항이 시작이면 1번 스티커를 건들지 않는다(N ~ 2).
이렇게 도출된 값 중 최대값이 정답이 된다.
3. 소스코드
#include <cstdio> #include <vector> using namespace std; int dp[100000][4]; inline int max(int a, int b) { return a > b ? a : b; } int solution(vector<int> sticker) { int answer = 0; int n = sticker.size(); if (n == 1) return sticker[0]; else if (n == 2) return max(sticker[0], sticker[1]); // [0] 앞부터 시작. 뜯지 않음. // [1] 앞부터 시작. 이번에 뜯음. // [2] 뒤부터 시작. 뜯지 않음. // [3] 뒤부터 시작. 이번에 뜯음. dp[0][0] = 0; dp[0][1] = sticker[0]; dp[n-1][2] = 0; dp[n-1][3] = sticker[n - 1]; for (int i = 1; i < n - 1; i++) { dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]); dp[i][1] = dp[i - 1][0] + sticker[i]; dp[n - 1 - i][2] = max(dp[n - i][2], dp[n - i][3]); dp[n - 1 - i][3] = dp[n - i][2] + sticker[n - 1 - i]; } int ret1 = max(dp[n - 2][0], dp[n - 2][1]); int ret2 = max(dp[1][2], dp[1][3]); answer = max(ret1, ret2); return answer; } int main() { // 입출력 예제 1 vector<int> v1 = { 14, 6, 5, 11, 3, 9, 2, 10 }; printf("%d\n", solution(v1)); // 입출력 예제 2 vector<int> v2 = { 1, 3, 2, 5, 4 }; printf("%d\n", solution(v2)); return 0; }
'알고리즘' 카테고리의 다른 글
| BOJ [1912] 연속합 (0) | 2017.09.10 |
|---|---|
| BOJ [1697] 숨바꼭질 (2) | 2017.09.10 |
| BOJ [9465] 스티커 (0) | 2017.09.10 |
| BOJ [1915] 가장 큰 정사각형 (0) | 2017.09.09 |
| BOJ [1051] 숫자 정사각형 (0) | 2017.09.01 |